질량이 m인 물체에 힘 F를 가했을 때, 물체는 가속도 a로 움직인다.
물체가 일정한 가속도 a로 움직일때, 이것을 등가속도 운동이라고 한다.

가속도 a의 값이 일정할 때, 가속도, 속도, 위치에 대한 그래프가 어떠한지 알아본다.
가속도 그래프
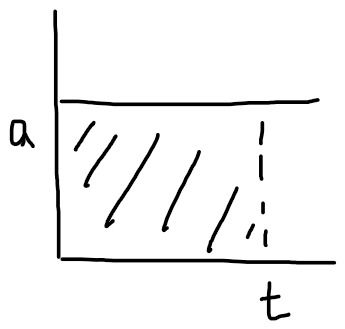
가속도 a는 시간에 따라 일정한 값이며, 시간 t에 대한 그래프의 면적은 속도의 변화량이 된다. (a * t)
속도 그래프

물체의 초기속도는 V0이며, 시간 t가 흘렀을떄의 속도는 V0+at이다. 그래프의 면적은 위치의 변화량이다. 이 면적은 사다리꼴이므로 이에 대한 변적을 구하면 아래와 같다.

위치 그래프

[속도 그래프] 상에서 시간 t에 대한 속도는 V0 + at 였다. 그리고 시간 t에 대한 위치의 변화량은 V0t+1/2a(t^2) 였다. 그러므로 초기 위치는 S0이며 시간 t가 흘렀을 때의 위치는 다음과 같다.

동 속도 운동?
등속도 운동은 가속도가 0인 운동을 의미한다. ( a = 0 ) 이를 위의 등가속도 운동 공식에 적용하면 다음과 같다.


지금까지 가속도(a), 시간(t), 속도(v), 거리(s)에 대해 다뤘다. 이에 대한 단위는 다음의 표와 같다.
| 문제 1 | |
초기 위치가 3m이며, 속도는 2m/s이다. 3초가 지난 후의 위치 s는?
가속도가 없으므로 이 물체는 등속도 운동을 한 것이다.

s = 3 + 2 * 3 = 9 이므로 위치 s는 9m이다.
문제 2
물체의 초기속도는 2m/s이고, 3m/s^2의 가속도를 가했을 때, 1초 뒤의 속도는 얼마인가?
이 물체는 등가속도 운동을 한다.

v = 2 + 3 * 1 = 5 m/s
문제 3
물체가 3m/s의 속도로 이동했고, 이때 위치는 초기 위치로부터 2m이다. 이 물체에 4m/s^2의 가속도가 가해졌다면 2 뒤의 위치는 얼마인가?

이 물체는 등가속도 운동을 한다.


포물선 운동
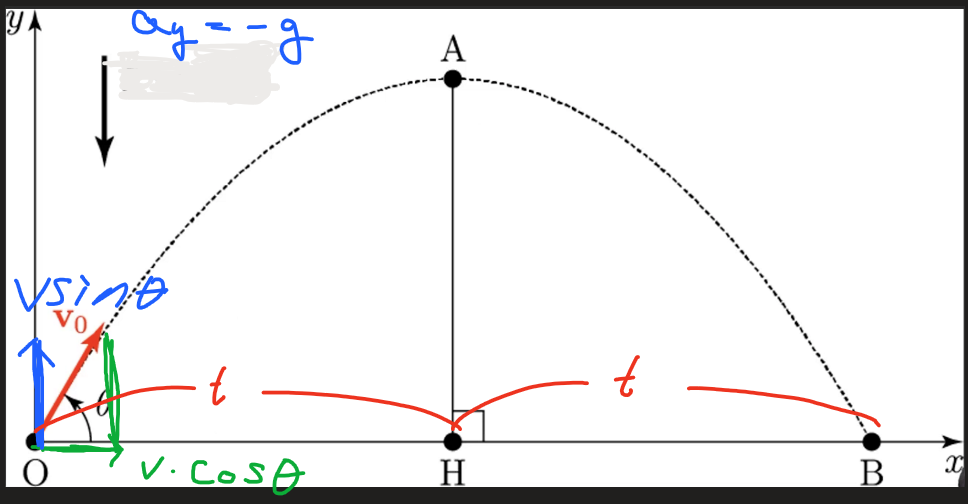
물체가 위치 (0, 0)에서 v0의 속도, theta의 각도로 날아갈 때, 이 물체는 포물선 그리며 이동한다. 이때, x와 y의 성분은 다음과 같다.
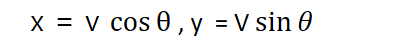
O, H, B의 위치에서 물체의 속도와 등가속도 공식이 어떻게 변화하는지 알아본다.
위치 O
이동을 시작하는 위치 이므로 위치 sx, sy는 0이다.


위치 H
중력 -g가 적용되고, 위치 H까지 이동하는데 시간 t가 흘렀다.
중력은 Y방향으로만 적용되므로 가속도는 0이며, 등속도 운동 공식이 적용된다.
최고점에 있으므로 속도는 0이다.


그런데 속도가 0이므로

위치 B
물체가 하강하고 있으므로 속도는 (-)이다.
날아간 거리는 위치 B의 X축의 값이며, 최고 높이는 위치 H의 Y 값이다.



'프로그래밍 이야기 > GameDev' 카테고리의 다른 글
| [게임이론] 마찰력과 저항력 (0) | 2021.01.19 |
|---|---|
| [게임이론] 등가속도 운동, 포물선 운동의 활용 (0) | 2021.01.18 |
| [게임이론] 힘과 가속도의 활용 (0) | 2021.01.14 |
| [게임이론] 힘과 가속도 (0) | 2021.01.10 |
| [게임이론] 행렬 (0) | 2021.01.02 |


