삼각함수는 각의 크기를 삼각비로 나타내는 함수이다. 다음의 삼각형에 대해 옛날에 배웠던 삼각함수 공식은 아래와 같다.
(입력 문제로 쎄타는 @로 표기한다.)

cos@ = a / c
sin@ = b / c
tan@ = b / a
그렇다면 c가 1이라고 가정하면, 아래와 같이 변한다.
cos@ = a / 1 = a
sin@ = b / 1 = b
tan@ = b / a
즉 밑변(a)의 길이는 cos@ 가 되고, 빗변(b)의 길이는 sin@가 된다. 이것을 피타고라스 정리에 대입해보면 다음과 같다

빗변의 길이가 1일때 벡터(방향)과 연계가 있기 때문에 잘 기억할 필요가 있다.
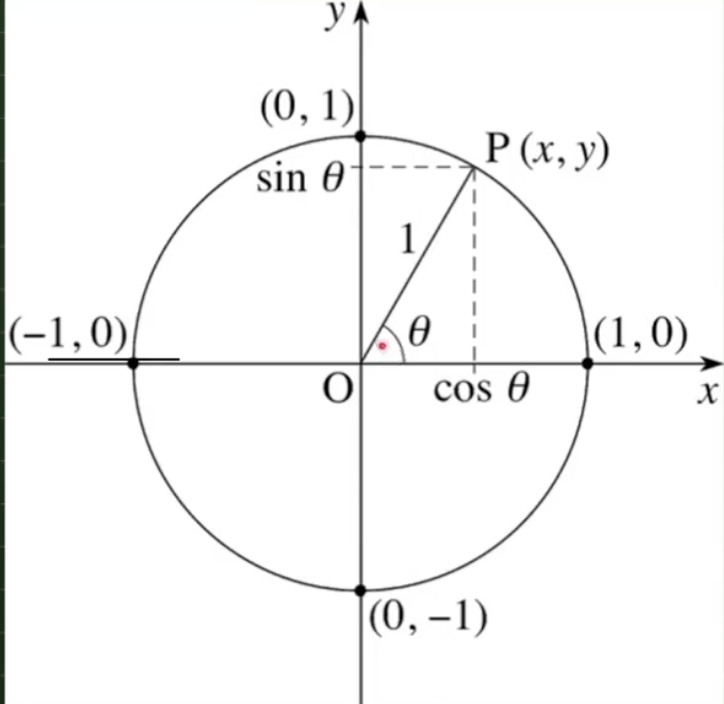
위와 같이 단위 원, 즉 반지름이 1인 원이 있다고 가정한다. 이 원에서 상의 가상의 위치 P(x, y)가 있다.
이 점을 통해 만들어지는 삼각형 상에서 밑변의 길이는 cos@, 높이는 sin@이다.
그러므로 x = cos@, y = sin@ 가 된다.
이 원 상에서 P(cos@, sin@) 로 표현 할 수 있다.
@가 0~360도로 움직일 때 cos@, sin@의 그래프는 아래와 같다.
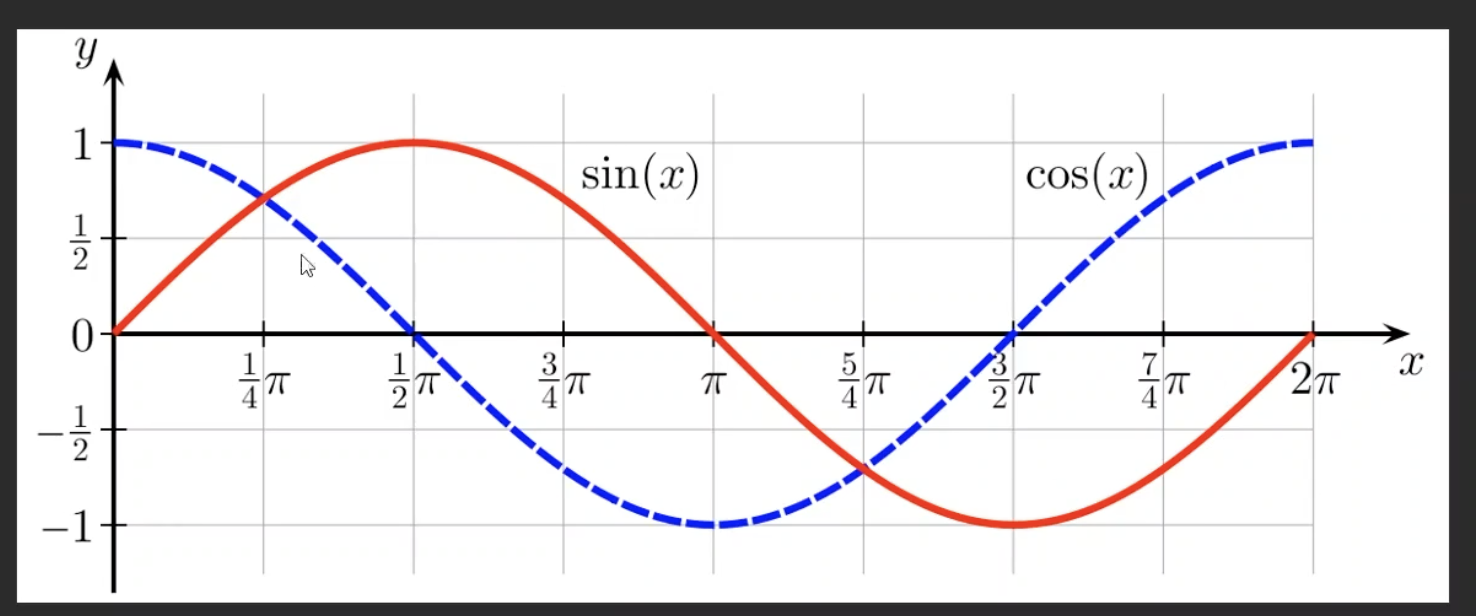
그렇다면 게임에서는?
단위 원 상에서 @가 30도라면 -> 점 P의 위치는 ( x: cos30, y : sin30 )
단위 원 상에서 @가 150도라면 ->점 P의 위치는 ( cos150, sin150)
일반화 하면, 담위 원상에서 @도라면 -> 점 P의 위치는 (cos@, sin@)
반지름 3인 원에서 @가 70도라면 -> (3*cos70, 3*sin70) 이 된다.
반지름이 n인 원에서 @도라면 -> (n*con@, n*sin@) 이다!
[게임이론] 삼각함수의 활용
definelife.tistory.com/search/%EC%82%BC%EA%B0%81 #define LIFE ZERO 인생 대 전환을 위한 기록, 프로그래밍과 IT 지식 소개 definelife.tistory.com 위의 삼각함수가 게임에서 어떻게 활용되는지 사례를 통해..
definelife.tistory.com
'프로그래밍 이야기 > GameDev' 카테고리의 다른 글
| [게임이론] 삼각함수의 활용 (0) | 2020.12.15 |
|---|---|
| [게임이론] Vector (0) | 2020.12.15 |
| [C#] File - BinaryFormatter (0) | 2020.12.08 |
| [C# 코딩연습] 임의의 성적표. 성적 추출 (0) | 2020.12.04 |
| [C#] Lamda, Func, Action (0) | 2020.11.29 |
